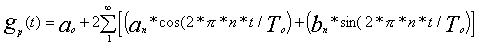
Fourier series is just a means to represent a periodic signal as an infinite sum of sine wave components. A periodic signal is just a signal that repeats its pattern at some period. The primary reason that we use Fourier series is that we can better analyze a signal in another domain rather in the original domain. Sometimes a signal reveals itself more in another domain.
In here, we will analyze the basic concept of fourier series. Let us assume that gp (t) is a periodic signal with period of To. With the use of fourier series, we can resolve the signal of gp (t) into an infinite sum of sine and cosine terms. After the Fourier series expansion of gp (t), the form is as the following:
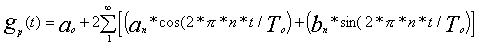
The terms an
and bn is the
unknown amplitude of the cosine and sine terms. Basically, fourier
series is used to represent a periodic signal in terms of cosine
and sine waves.
Let's demonstrate a bit with an example of a periodic wave
and extract the appropriate sine wave from it by using a band-pass
filter at the right frequency. Figure 1 contains a graph that
has a combination of sine waves.
Figure 1. Periodic wave

The above periodic wave is made up the sum of the following
waves. Figure 2 is a wave that has a frequency of 10 Hz. Figure
3 is another sine wave with frequency of 20 Hz. Lastly, figure
4 is just another sine wave at a frequency of 30 Hz.
Fig. 2. Sine wave 10 Hz.
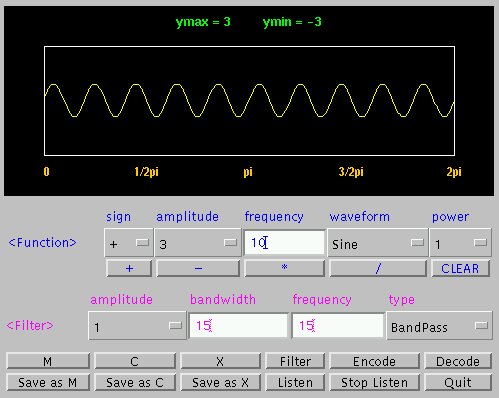
Fig. 3. Sine wave 20 Hz
Fig. 4. Sine wave at 30 Hz.
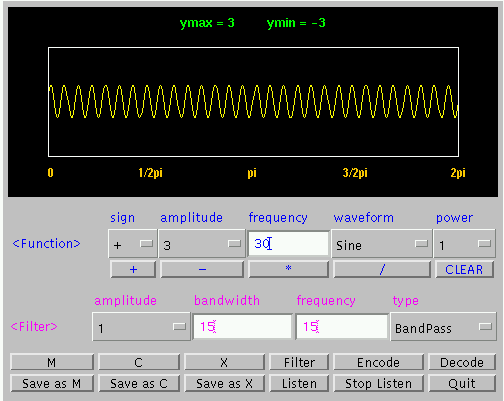
As mentioned before, we can use a band-pass filter to extract
the different components from the periodic wave. The following
are the results of the extraction from the periodic wave.
Fig 5. Extraction of 10 Hz Sine Wave from Sum Wave
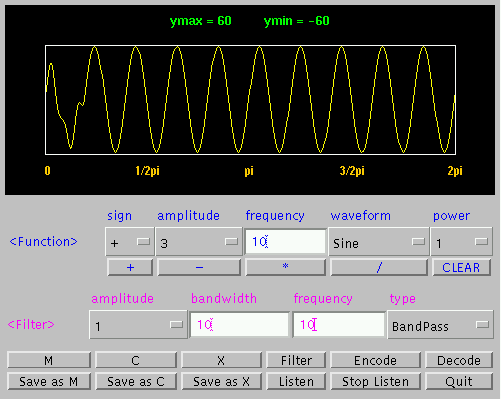
Fig 6. Extraction of 20 Hz Sine Wave from Sum Wave
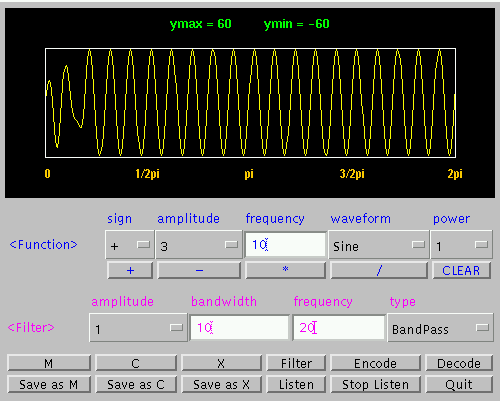
Fig. 7. Extraction of 30 Hz Sine Wave from Sum Wave
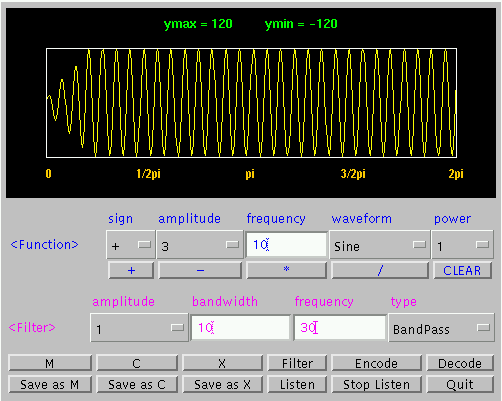
The above example shows that any periodic signal is just a combination of sine and cosine waves. Fourier series is a method to represent that periodic signal that we can manage it easily with simple trigonometry skills.